Limits

First Principles of Differentiation
Continuity

There's still a limit at a point if there's a hole at the point
Limits do not exist at discontinuities, unbounded points, or infinitely oscillating points
Squeeze theorem: If $f (x) \leq g (x) \leq h (x)$ , and $lim_{x \to a} f (x) = lim_{x \to a} h (x) = L$ , then $lim_{x \to a} g (x) = L$
- If you use this, and have a step with a potentially negative function, make sure to take cases where the function is positive and negative

Proof of

lim_{θ \to 0} \frac{\sin θ}{θ} = 1

\begin{aligned} A_{△ O A P} & < A_{O A P} & < A_{△ O A T} \\ \frac{1}{2} \sin θ & < \frac{θ}{2} & < \frac{\tan θ}{2} \\ 1 & < \frac{θ}{\sin θ} & < \frac{1}{\cos θ} \\ 1 & > \frac{\sin θ}{θ} & > \cos θ \\ lim_{θ \to 0} 1 & > \frac{\sin θ}{θ} & > 1 \end{aligned}

If $f$ is continuous at $b$ and $lim_{x \to a} g (x) = b$ , then $lim_{x \to a} f (g (x)) = f (lim_{x \to a} g (x)) = f (b)$ , provided $f (g (x))$ is defined on an interval containing $a$

L'Hôpital's Rule

Solving Tips

If your limit has a trig function in it, start with $- 1 \leq \sin θ \leq 1$ , then squeeze
If there is a $\frac{1}{x}$ , try getting the limit from both sides of 0, and see if they're the same
Try to "force" out a factor
- If you take a square out of a square root, use the absolute value. This means if the limit value is negative, negate the x
Try to force a $\frac{\sin x}{x}$ or $\frac{\tan x}{x}$ scenario
- you can try to do this by dividing the top and bottom of a fraction by x
multiply by conjugate sometimes
If you have infinities, try to make it $\frac{1}{x}$ so it's 0s instead

Formal Definition (Epsilon-delta)

Formal Definition

$f (x)$ approaches the limit $L$ as $x$ approaches $a$
$lim_{x \to a} f (x) = L$
If this holds:
$\forall ϵ > 0$ (very small number), $\exists δ > 0$ , depending on $ϵ$ , such that $0 < | x - a | < δ ⟹ | f (x) - L | < ϵ$
In english, if you get some small y-range of a function, you can get a small x-range, such that when you evaluate the x-range, the values are in between the y-range
$ϵ$ is like your tolerance

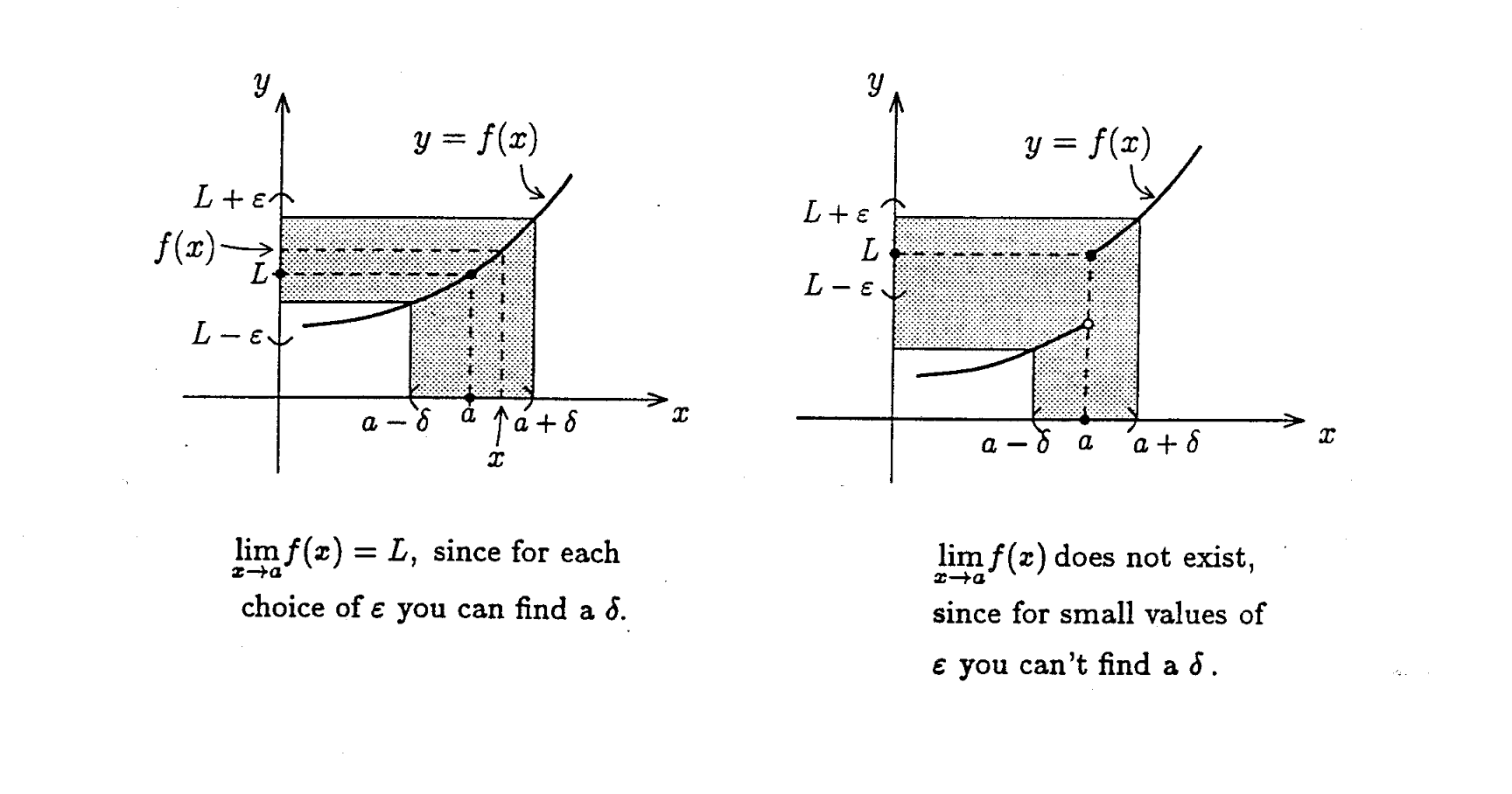
To prove a limit exists:
- Start with the $| f (x) - L | < ϵ$ , then try to get to $0 < | x - a | < δ$
  - the $0 < | x - a |$ implies that $x \neq a$
When you get two values for $δ$ (one on either side of $a$ ), take the smaller one

Single example

Find $δ$ such that $| x^{2} - 25 | < 1$ whenever $| x - 5 | < δ$
We realize $f (x) = x^{2}, L = 25, ϵ = 1, a = 5, lim_{x \to 5} x^{2} = 25$

\begin{aligned} | x^{2} - 25 | & < 1 \\ - 1 & < x^{2} - 25 < 1 \\ 24 & < x^{2} < 26 \\ \sqrt{24} & < | x | < \sqrt{26} \\ \sqrt{24} & < x < \sqrt{26} ∵ x \approx 5 \\ \sqrt{24} - 5 & < x - 5 < \sqrt{26} - 5 \\ | \sqrt{24} - 5 | & < | x - 5 | < | \sqrt{26} - 5 | \end{aligned}

Full proof

Prove that $lim_{x \to 5} x^{2} = 25$
Show that $\forall ϵ > 0, \exists δ > 0$ s.t. $0 < | x - 5 | < δ ⟹ | x^{2} - 25 | < ϵ$
Begin by rewriting in terms of $x - 5$

\begin{aligned} | x^{2} - 25 | & = | (x - 5)^{2} + 10 (x - 5) | \\ \leq | x - 5 |^{2} + 10 | x - 5 | by triangle inequality \\ < δ^{2} + 10 δ ∵ δ > | x - 5 | \\ δ^{2} + 10 δ & = ϵ \\ δ^{2} + 10 δ - ϵ & = 0 \\ δ & = - 5 \pm \sqrt{25 + ϵ} \\ ∵ δ > 0, δ & = - 5 + \sqrt{25 + ϵ} \\ ∴ \forall ϵ > 0, \exists δ > 0 \end{aligned}

Alternate solution (if it's not a solvable quadratic)

\begin{aligned} | x^{2} - 25 | & < δ^{2} + 10 δ \\ δ^{2} & < δ ∵ δ is small \\ | x^{2} - 25 | & < δ + 10 δ \\ < 11 δ \\ = ϵ \\ δ & = \frac{ϵ}{11} \end{aligned}

Limits of Multivariable Functions

For a function with 2 variables $f (x, y)$ , $lim_{(x, y) \to (a, b)} f (x, y) = L$ means that $f (x, y)$ approaches $L$ for all possible paths
This means from every direction, the limit goes to $L$
It is easier to show that a limit doesn't exist by counterexample (choose two directions that approach a different value)
- You can also set $y = m x$ and show that $lim_{(x, m x) \to (a, b)} f (x, m x)$ depends on $m$
  - This works since you're doing like a line so you're approaching from every possible direction
  - This doesn't actually prove that the limit exists though (for example, you could do $x = y^{2}$ and it could give a different value)
Usually proving a limit involves the squeeze theorem, but sometimes is possible with algebra